Predictive Maintenance für Medizinische Geräte (Teil 2)
April 25, 2018
In Teil 1 dieser Fallstudie haben wir ein allgemeines Problem in der Ära von Industrie 4.0 eingeführt, wo ein Hersteller von medizinischen Geräten künstliche Intelligenz einsetzen möchte, um mögliche Fehler seiner Geräte vorherzusagen, bevor sie auftreten. Wir haben auch die Art und Weise beschrieben, wie wir historische Sensordaten mit drei medizinischen Geräten vorverarbeitet haben. In diesem Artikel werden vier ML-Klassifikatoren erstellt, um aus diesen Daten zu lernen. Anschließend bewerten wir die Leistung jedes Modells, um die Ergebnisse von nicht beobachteten Ereignissen vorherzusagen.
1. Datenaggregation
In diesem Schritt aggregieren wir Daten aller Geräte in einem einzigen Datenrahmen. Basierend auf der Ausgabe von PCA auf den drei Geräten berücksichtigen wir nur die ersten 6 PCs jedes Ereignisses, da die verbleibenden PCs dem Klassifizierungsprozess keine zusätzlichen Informationen hinzufügen. Die ausgewählten PC-Dimensionen werden in [0,1] für jedes Gerät normalisiert und zu einem einzigen Datenrahmen aggregiert. Zusätzlich wenden wir eine einfache Gleitender Mittelwert Prozedur für jede Klasse (Normal, Warnung, Alarm) separat an. Die folgende Abbildung zeigt aggregierte Daten nach Anwendung des einfachen Gleitenden Mittelwert, projiziert von den ersten beiden PCs.
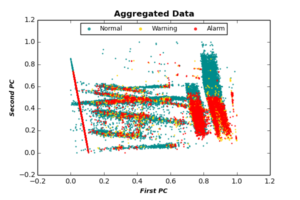
2. Ungleichgewicht der Datenklassen
Unausgeglichene Datenklassen sind in vielen Geschäftsbereichen von Data Science ein häufiges Problem, und Thema “Predictive Maintenance” ist keine Ausnahme. In unserem Fall repräsentiert die Hauptkategorie der Beobachtungen “Normal” Ereignisse, bei denen die Geräte ordnungsgemäß laufen. Diese Klasse wird normalerweise als negative Klasse bezeichnet. Die interessierenden Klassen sind jedoch diejenigen Klassen, die vorhergehenden Fehlern vorangehen (d. H. Die positiven Klassen). Das folgende Diagramm zeigt die Verteilung unserer drei Klassen über alle Geräte. Es zeigt, dass sowohl die “Warning” – als auch die “Alarm” Klasse fast 28% der Daten repräsentieren.
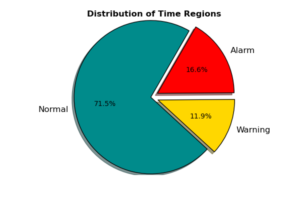
In dieser Studie werden wir unsere Daten nicht durch Upsampling die Minoritätsklassen oder Downsampling der Hauptklasse ausgleichen. Dies liegt daran, dass unsere ML-Modelle Minoritätsklassen richtig lernen können (siehe unten). Wenn es für Klassifikatoren jedoch schwierig ist, aus unausgeglichenen Klassen zu lernen, wird empfohlen, die Daten vor den Klassifizierungseinheiten zu balancieren. Eine beliebte Technik zur Behandlung von unausgewogenen Datenklassen ist der Upsampling-SMOTE [1] Algorithmus.
3. Mehrklassige Klassifikation
Um Fehlschläge vorherzusagen, trainieren wir vier Klassifizierer für mehrere Klassen: logistische Regression (Log. Regression), K-Nächste Nachbarn (KNN), Mehrklasse Neural Network (NN) und Random Forest (RF). Um eine Überanpassung an bestimmte Testdaten zu vermeiden, wurde jeder Klassifikator aufgrund seines durchschnittlichen Validierungswerts im Vergleich zu einem 10-fachen Kreuzvalidierungsverfahren einem Benchmark unterzogen. Die folgende Abbildung zeigt Konfusionsmatrizen der vier Klassifikatoren.
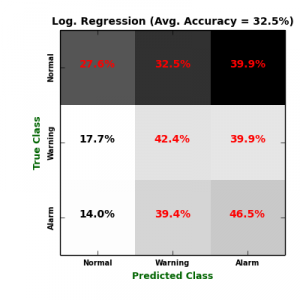
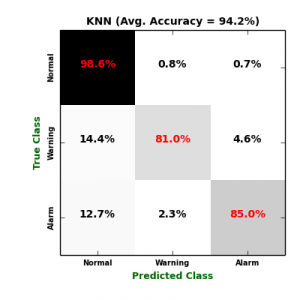
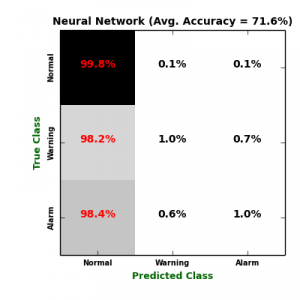
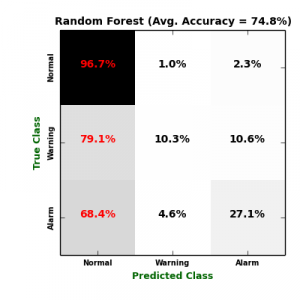
Auf der einen Seite ist es offensichtlich, dass KNN das sensibelste Modell für die Minoritätsklassen (“Warnung” und “Alarm“) erzeugt, gefolgt von der logistischen Regression. Das Problem mit dem logistischen Regressionsmodell besteht darin, dass es die Hauptklasse “Normal“, die seine False Positive (FP) Rate maximiert, weitgehend falsch klassifiziert hat. Auf der anderen Seite erkennen sowohl NN- als auch RF-Klassifikatoren die “Warning” – und “Alarm” -Klassen nicht, was ihre False Negative (FN) Raten maximiert. Die folgende Tabelle enthält weitere Validierungsmetriken, die aus Konfusionsmatrizen berechnet wurden. \begin{array}
{|c|c|c|c|c|}
\hline Metric & Log. Reg. & KNN & NN & RF \\\hline
\hline Accuracy\ Avg. & 0.325 & {\bf 0.942} & 0.716 & 0.748 \\\hline
\hline Accuracy\ Std. & 0.004 & 0.001 & {\bf 0.0} & 0.001 \\\hline
\hline F1\ Avg. & 0.299 & {\bf 0.905} & 0.289 & 0.467 \\\hline
\hline F1\ Std. & 0.004 & {\bf 0.003} & 0.006 & 0.005 \\\hline
\hline Avg.\ Macro\ Recall & 0.38 & {\bf 0.93} & 0.53 & 0.61 \\\hline
\hline Avg.\ Macro\ Precision & 0.38 & {\bf 0.88} & 0.34 & 0.45\\\hline
\hline Avg.\ Micro\ Recall/precision & 0.33 & {\bf 0.94} & 0.72 & 0.75 \\\hline
\end{array}
Wie die Tabelle zeigt, übertrifft das KNN-Modell die drei anderen Modelle über alle Validierungsmetriken hinweg. In dieser Tabelle ist Accuracy Std. und F1 Std. für Genauigkeit und F1-Standardabweichungen über die 10-fachen Kreuzvalidierungsmodelle stehen. Die niedrigste Standardabweichung, das stabilste Modell für den Einsatz.
4. Binäre Klassen Auswertung
Neben der Validierung unserer vier Klassifikatoren in mehreren Klassifikationseinstellungen möchten wir sie als binäre Klassifikatoren bewerten. Das Ziel besteht darin, zu messen, wie jeder Mehr-klassen Klassifikator abläuft, wenn er als Binärklassifizierer ausgeführt wird. In diesem Abschnitt werden wir nicht jeden Klassifizierer mit binär gekennzeichneten Daten neu trainieren. Stattdessen werden wir die obigen Verwirrungsmatrizen in 2D-Matrizen umwandeln, indem “Normal” und “Warning” -Klassen als eine einzige Mehrheitsklasse (d. H. Negativ) und “Alarm” -Klasse als Minoritätsklasse (d. H. Positiv) betrachtet werden. Danach werten wir alle Klassifikatoren als binäre aus.
4.1 ROC-Kurve
Ein nettes Visualisierungswerkzeug zum Bewerten binärer Klassifikatoren ist das Aufzeichnen der Beziehung zwischen den “True Positive” (TP) und den “False Positive” (FP) Raten. Die erste Rate gibt an, wie viele “Alarm” Ereignisse korrekt als “Alarm” vorhergesagt wurden, während die letztere Rate bestimmt, wie viele “Normal” und “Warning” Ereignisse fälschlicherweise als “Alarm” vorhergesagt wurden. Die Signifikanz von ROC-Kurven ist, dass sie die Fähigkeit jedes Klassifikators anzeigen, die Minderheitsklasse korrekt vorherzusagen (d. H. “Sensitivität“) und inwieweit diese Sensitivität die Fähigkeit zur korrekten Vorhersage der Majoritätsklasse beeinflusst (d. H. “Spezifität“)
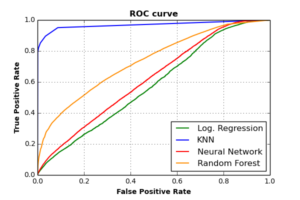
Wir können die Sensitivität / Spezifität jedes Klassifikators messen, indem wir die Fläche unter der ROC-Kurven (AUC) messen. Wie in der obigen Grafik zu sehen ist, hat der KNN-Klassifikator den größten AUC-Score (0.97). Dies bedeutet, dass der KNN-Klassifikator eine extrem hohe Sensitivität erreichen kann, während er genaue Spezifitätsraten beibehält. Der AUC-Wert für den RF-Klassifikator ist (0.73), für NN ist (0.62) und für Log. Regression ist (0.58).
4.2 Recall-Precision Kurve
Ein weiteres interessantes Auswertungsdiagramm ist dasjenige, das die Abwägung von Recall und Präzision für Differenzschwellwerte jedes Klassifikators beschreibt. Klassifikatorschwelle ist der Wert, bei dem jeder Klassifikator die Bezeichnung (d.H. die Klasse) jedes Ereignisses basierend auf dem probabilistischen Gewicht, das er von jeder Klasse erhält, bestimmt. Das folgende Diagramm zeigt die Recall-Precision-Kurven der vier Klassifikatoren.
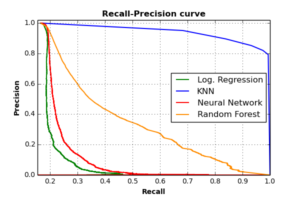
Wie die Grafik zeigt, erreichen alle Klassifikatoren hohe Genauigkeitsraten, wenn der Trefferquote niedrig ist. Wenn der Trefferquote zunimmt, verschlechtern sich die Genauigkeitsraten für RF-, NN- und logistische Regressions-Klassifizierer. Der KNN – Klassifikator kann jedoch hohe Genauigkeitsraten (um 0.9) mit sehr hohen Trefferquote (etwa 0.8) erreichen, was KNN gegenüber anderen Klassifikatoren schläg auch dieses Bewertungskriterium.
4.3 Kalibrierungskurve
Das Kalibrierungsdiagramm ist ein weiteres nützliches Visualisierungswerkzeug zum Messen der Häufigkeitserwartung von Klassifizierern. Die Kalibrierungskurve eines Klassifikators spiegelt die Korrelation zwischen dem Anteil der als positiv bewerteten Ereignisse der positiven Klasse, und der vorhergesagten Wahrscheinlichkeit der positiven Klasse wider. Gute kalibrierte Klassifikatoren sollten eine hohe Korrelation zwischen den beiden Skalen aufweisen.
Im Falle eines perfekt kalibrierten Klassifikators (einer, der der diagonalen Linie in der unteren Grafik folgt), wenn der Klassifikator entscheidet, dass eine bestimmte Menge von Ereignissen positiv ist (d. H. “Alarm” -Ereignisse) mit einer durchschnittlichen Wahrscheinlichkeit von 0.75, dann wenn wir alle Ereignisse sammeln Bei einer Wahrscheinlichkeit von 0.75 sollten 75% dieses Teils eine echte Bezeichnung “Alarm” haben. Das folgende Diagramm zeigt Kalibrierkurven der vier Klassifikatoren.
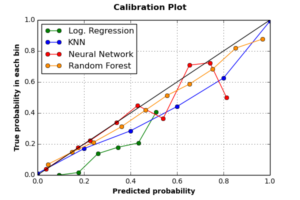
Die Grafik zeigt, dass RF der am besten kalibrierte Klassifikator ist, gefolgt von KNN. Obwohl alle Klassifikatoren die wahre Wahrscheinlichkeit von Beobachtungen unterschätzt haben, erreichen RF und KNN Klassifikatoren akzeptable probabilistische Schätzungen der positiven Klasse. Der am schlechtesten kalibrierte Klassifikator ist die logistische Regression, da er es versäumt hat, irgendeine positive Beobachtung korrekt zu schätzen, gefolgt von dem NN Klassifikator, der die Wahrscheinlichkeiten der negativen Klasse perfekt geschätzt hat, aber falsch mit der positiven Klasse lief.
4.4 Erwartete Kosten
Die letzten Bewertungskriterien in dieser Studie werden als erwartete Kosten [2] bezeichnet. Erwartete Kosten (oder erwarteter Nutzen) ist eine genaue Metrik, um binäre Klassifikatoren zu bewerten. Bedeutung von Erwartete Kosten besteht darin, dass es die korrekten und fehlerhaften Vorhersagen des Klassifikators mit den entsprechenden Vorteilen und Kosten jeder Vorhersage verknüpft. Basierend auf den Geschäftszielen des Benutzers können Experten jeder Geschäftsdomäne den Einfluss jeder Vorhersage abschätzen (richtig negativ (TN), falsch negativ (FN), falsch positiv (FP) und richtig positiv (TP)). Typischerweise werden die Geschäftskonsequenzen, die auf korrekten Vorhersagen beruhen, “Vorteile” genannt, während diejenigen von falschen Vorhersagen “Kosten” genannt werden. In dieser Studie weist der Hersteller 0.5 Vorteile von richtig Negativen, 0.99 Vorteile von richtig positiven, 0.4 Kosten von falsch positiven Ergebnissen und 0.99 Kosten von falsch negativen Bewertungen. Die Formel für die erwarteten Kosten lautet wie folgt:
\begin{equation}
\begin{split}
Expected\ Cost = P(\mathbf{p})\times [P(TP)\times \textit{benefit}(TP) + P(FN)\times \textit{cost}(FN)] \\
+\ P(\mathbf{n})\times [P(TN)\times \textit{benefit}(TN) + P(FN)\times \textit{cost}(FP)]
\end{split}
\end{equation}
Die Werte \(P(\mathbf{p})\) und \(P(\mathbf{n})\) repräsentieren die Wahrscheinlichkeiten der positiven bzw. negativen Klassen, und die Werte \(P(TP), P(FN), P(TN)\) und \(P(FN)\) repräsentieren die Wahrscheinlichkeiten der vier Typen der Klassifikatoren Vorhersagen. Durch Berechnen der erwarteten Kosten der obigen vier Klassifizierer bewertet KNN die niedrigsten Kosten mit 0.61, gefolgt von Log. Regression (0.69), RF (0.81) und NN (0.99).
Dies bedeutet, dass die Verwendung des KNN-Klassifikators aus Sicht des Herstellers die Betriebskosten, seiner medizinischen Geräte am besten minimiert. Basierend auf dieser Tatsache und allen anderen obigen Bewertungsmetriken, empfehlen wir den KNN-Klassifikator als den besten geeigneten Klassifizierer für diese Fallstudie.
5. Abschluss
In dieser Fallstudie trainierten wir vier Klassifikatoren, um die “Alarm” Ereignisse historischer Sensordaten von drei medizinischen Geräten zu erfassen. Die Auswertung von die vier Klassifikatoren zeigt an, dass das KNN die drei anderen Klassifikatoren in fast allen Bewertungsmetriken und Kurven übertrifft. Weitere Optimierungen können durchgeführt werden, um die Leistung von KNN zu verbessern. Wie zum Beispiel die Optimierung der Anzahl der nächsten Nachbarn k, oder das Hinzufügen einer Kalibrierungsfunktion, um die Kalibrierung zu verbessern. Andere Klassifikatoren können auch in größeren Benchmarking Einstellungen hinzugefügt werden, um die Zuverlässigkeit der Klassifikatorauswahl zu erhöhen.
[1] N. V. Chawla, K. W. Bowyer, L. O. Hall, and W. P. Kegelmeyer (2002). SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research, 16(1), 321-357.
[2] F. Provost and T. Fawcett (2013). Data Science for Business (Chapter 7). O’Reilly Media, Inc.


Your web site has exceptional content. I bookmarked the site
Thanks!
Do you have any type of tips for composing posts?
That’s where I constantly battle as well as I simply wind up looking vacant screen for very long time.
As a kick-off material, you can see the following YouTube Videos:
1- How To Make a WordPress Website – 2017 – Create Almost Any Website! (https://www.youtube.com/watch?v=xiB0HPMy4GE)
2- How to Design a WordPress Single Post Template with Elementor (https://www.youtube.com/watch?v=yLWLd705c3Q)