Predictive Data Analytics With Apache Spark (Part 5 Regression Analysis)
January 15, 2019
1. Import Parquet Data Files into Spark Dataframes
At the end of the previous Post we saved our train and test Dataframes as .parquet data files. Now we want to retrieve these files as Spark Dataframes. The following code lines achieve this job.
from pyspark import SQLContext
# create SQLContext object to read Parquet files (support also JSON and JDBC data sources)
sqlContext = SQLContext(sc)
# Load data from file 'train_FD001_preprocessed.parquet'
train_df = sqlContext.read.parquet(os.getcwd() + '/' + path + 'train_FD001_preprocessed.parquet')
test_df = sqlContext.read.parquet(os.getcwd() + '/' + path + 'test_FD001_preprocessed.parquet')
2. Calculate Correlations Between Features
The first step in building regression models is to find the suitable subset of data features for regression analysis. The easiest way of selecting those features is to calculate the correlation between the target variable (in our use case, Engine’s Remaining Useful Life “RUL” ), and independent variables (all native and generated data features explained in the previous two Posts). The following function calculates Pearson correlation between both sides.
from pyspark.ml.feature import VectorAssembler
from pyspark.ml.stat import Correlation
def get_correlations(df, features):
'''
this function returns list of correlations of numerical features of PySpark Dataframe
INPUTS:
@df: PySpark Dataframe
@features: list of columns' names to calculate correlations in between
OUTPUTS:
@sorted_corr_dict: list of @df feautres sorted by their correlations to the first feature
'''
# convert to vector column first
vector_col = "corr_features"
assembler = VectorAssembler(inputCols= features, outputCol=vector_col)
df_vector = assembler.transform(df).select(vector_col)
# get correlation matrix
r1 = Correlation.corr(df_vector, vector_col).head()
# get list of Pearson correlations between first feature (RUL) and all other features
corr_list = r1[0].toArray()[:1,:].tolist()[0]
# set dictionary of features and correlations
corr_dict = dict(zip(corr_list, input_features))
# sort dictionary by Pearson correlations
sorted_corr_dict = sorted(corr_dict.items(), key=operator.itemgetter(0))
return sorted_corr_dict
We execute the above function using the following code:
# get Pearson correlations between RUL and other numerical features
train_ulr_corr = get_correlations(train_df, input_features)
test_ulr_corr = get_correlations(test_df, input_features)
# print top positive correlated features
print("Top Positive Correlated Features (Train):\n")
for i in reversed(train_ulr_corr[-6:-1]):
print(i)
print("\nTop Positive Correlated Features (Test):\n")
for i in reversed(test_ulr_corr[-6:-1]):
print(i)
# print top negative correlated features
print("\nTop Negative Correlated Features (Train):\n")
for i in train_ulr_corr[0:5]:
print(i)
print("\nTop Negative Correlated Features (Test):\n")
for i in test_ulr_corr[0:5]:
print(i)
Following is the output of these lines:
Top Positive Correlated Features (Train):
(0.7891290976368206, 's12_rollingmean_4_scaled')
(0.7797179646508305, 's7_rollingmean_4_scaled')
(0.7743707880518276, 's12_rollingmean_4_norm')
(0.7733777137249406, 's7_rollingmean_4_norm')
(0.7117150656675688, 's12_rollingmean_4')
Top Positive Correlated Features (Test):
(0.54098279911739, 's12_rollingmean_4_norm')
(0.49366782512940416, 's7_rollingmean_4_norm')
(0.4751862708553446, 's12_rollingmean_4_scaled')
(0.4585230500478898, 's7_rollingmean_4_scaled')
(0.2875254965000236, 'PCA_2_scaled')
Top Negative Correlated Features (Train):
(-0.7888110654218343, 's4_rollingmean_4_scaled')
(-0.7757296788046874, 's4_rollingmean_4_norm')
(-0.7466390619110802, 's17_rollingmean_4_scaled')
(-0.7451601569134584, 's2_rollingmean_4_scaled')
(-0.7332185343637497, 's3_rollingmean_4_scaled')
Top Negative Correlated Features (Test):
(-0.5202779694027116, 'PCA_5_scaled')
(-0.5202779694027094, 'PCA_5_norm')
(-0.5202779694012791, 'PCA_5')
(-0.5094505130758384, 's4_rollingmean_4_norm')
(-0.4636488921403958, 's4_rollingmean_4_scaled')
CPU times: user 33.9 ms, sys: 13.4 ms, total: 47.3 ms
Wall time: 9.49 s
3. Build Features Vector of Train Dataframe
After obtaining the best correlated features to out target variable (RUL), we build the features vector of our train dataset. This vector will be used as the train data vector in all regression algorithms.
# select features to be used into regression algorithms
train = train_df.select(train_df["s12_rollingmean_4_norm"],train_df["s7_rollingmean_4_scaled"],
train_df["s12_rollingmean_4_scaled"],train_df["s4_rollingmean_4_norm"],
train_df["s4_rollingmean_4_scaled"],train_df["rul"])
# build train features vector
train_vector = train.rdd.map(lambda x: [x[5], Vectors.dense(x[0:5])]).toDF(['label','features'])
We selected here 5 independent features to build the training vector. You are free to select more or less number of features as you wish. Please note that we add the dependent variable “URL” at the end of our training vector. Please note also that the set of independent variables should be full compatible in both train and test vectors. The test vector will be build during the regression modeling below.
4. Linear Regression
4.1 Initialize Linear Regression Instance
The first step in regression analysis is to set new instance of LinearRegression() function:
from pyspark.ml.regression import LinearRegression
# init LR instance
lr = LinearRegression(featuresCol = 'features', labelCol = 'label', maxIter=100)
As you notice in the above line, we pass the names we defined in training data vector for independent features (“features“) and target variable (“label“) to LinearRegression() function. We also set the maximum number of iterations of the LR algorithm to 100.
4.2 Optimize Model Parameters
If you want to change the default parametric settings of LinearRegression() function above, you can do so by changing the parametric settings when initializing the object:
# init LR instance
lr = LinearRegression(featuresCol = 'features', labelCol = 'label',
regParam=0.2, elasticNetParam=0.5, maxIter=200)
In the above line, we set the maximum iterations to 200, the regression parameter to 0.2, and the elastic net parameter to 0.5.
4.3 Fit Linear Regression Model to Training Data Vector
The second step is to fit the LR model to our train data vector.
# fit linear regression model
lr_model = lr.fit(train_vector)
Here we build our regression model by passing train data vector to the LR instance created in the previous step.
4.4 Build Test Features Vector
The third step is to build test data vector compatible to the train vector:
# select test features (with same features set as of train vector)
test = test_df.select(test_df["s12_rollingmean_4_norm"],test_df["s7_rollingmean_4_scaled"],
test_df["s12_rollingmean_4_scaled"],test_df["s4_rollingmean_4_norm"],
test_df["s4_rollingmean_4_scaled"],test_df["rul"])
# build test features vector
test_vector = test.rdd.map(lambda x: [x[5], Vectors.dense(x[0:5])]).toDF(['label','features'])
4.5 Get Predictions
After executing the above steps, we can obtain predictions by passing the test vector to the regression model:
# get predictions pred = lr_model.transform(test_vector)
4.6 Evaluate Regression Model
As we have build our regression model and applied it to the test dataset, we can evaluate our regression model. Apache Spark has some nice functions that calculate basic evaluation metrics of regression models. To make use of it, we need to initialize an evaluation object:
from pyspark.ml.evaluation import RegressionEvaluator
# initialize regression evaluation instance
evaluator = RegressionEvaluator(predictionCol='prediction', labelCol='label')
Now we can use this evaluation instance to calculate some nice evaluation metrics. The following lines of code prints R Squared, Mean Square Error (MSE), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE).
# print evaluation metrics
print "R-squared= ", evaluator.setMetricName('r2').evaluate(pred)
print "MSE= ", evaluator.setMetricName('mse').evaluate(pred)
print "RMSE= ", evaluator.setMetricName('rmse').evaluate(pred)
print "MAE= ", evaluator.setMetricName('mae').evaluate(pred),
4.7 Visualize Evaluations
By applying the above steps to a subset of Engines (Engines 18, 30, 38, 12, 34), we obtained evaluation results as plotted below.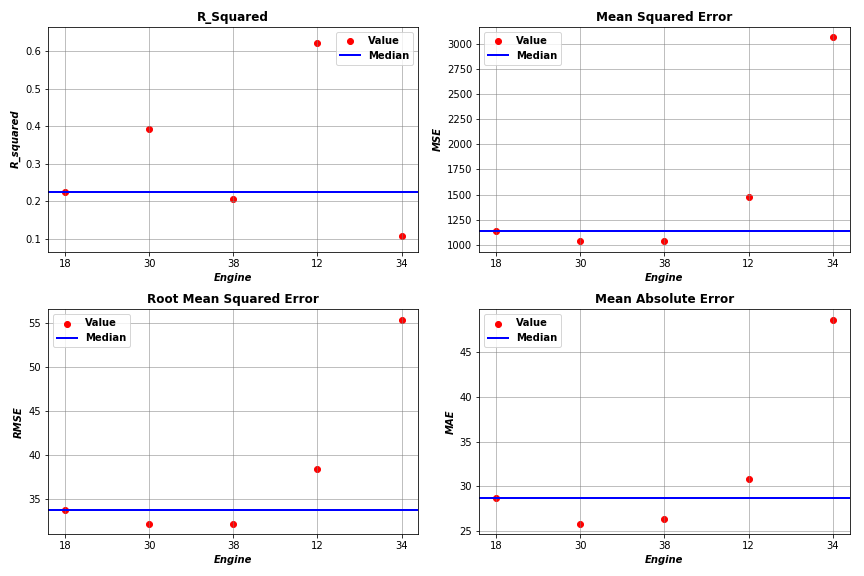
5. Generalized Linear Regression
5.1 Initialize Generalized Linear Regression Instance
By following the same steps above, we can build another regression model called Generalized Linear Regression using the below code:
from pyspark.ml.regression import GeneralizedLinearRegression
# init GLR instance
glr = GeneralizedLinearRegression(featuresCol = 'features', labelCol = 'label', family="gaussian",
link="identity", maxIter=50, regParam=l)
Where regression parameter \(l\) can take one of the values [0, 0.5, 1, 10, 30, 50].
5.2 Visualize Evaluations
By evaluating the above model using different input parameters’ settings, we can compare the model performance using each setting and select the most accurate one.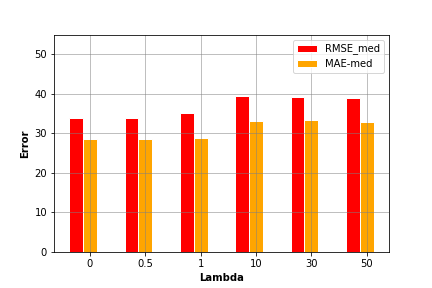 In the above plot, we find that setting regression parameter to 0 generates the lowest error values.
In the above plot, we find that setting regression parameter to 0 generates the lowest error values.
6. Decision Tree
6.1 Initialize Decision Tree Regression Instance
The last regression model in this post is the Decision Tree algorithm. Within this algorithm, we will optimize two parameters of decision tree; namely, the max number of bins (i.e. enables more feature partitioning) and max depth (i.e. the length of the longest path from the root to a leaf).
from pyspark.ml.regression import DecisionTreeRegressor
# set tree max. depth
maxDepth = [5, 10]
# set tree max. number of bins
maxBins = [4, 8]
# build and evaluate decision tree regression model
for m1 in maxDepth:
for m2 in maxBins:
# init decision tree instance with parameters
dt = DecisionTreeRegressor(featuresCol = 'features', labelCol = 'label',
maxDepth=m1, maxBins=m2)
6.2 Evaluation
By evaluating Decision Tree model, we calculate R-Squared, MSE, RMSE, and MAE metrics. The results are as follows:
maxDepth = 5 max Bins = 4
median R-Squared: 0.2109488013465084
median MSE: 2021.0993725649312
median RMSE: 44.956638804129156
median MAE: 34.39000675943137
maxDepth = 5 max Bins = 8
median R-Squared: 0.2587368658296212
median MSE: 1949.072147238039
median RMSE: 44.14829721787737
median MAE: 36.04739104979992
maxDepth = 10 max Bins = 4
median R-Squared: 0.2615910842192609
median MSE: 2361.48434721602
median RMSE: 48.595106206448605
median MAE: 39.69089356011583
maxDepth = 10 max Bins = 8
median R-Squared: 0.1925103581215516
median MSE: 2983.7077209127956
median RMSE: 54.623325795055685
median MAE: 44.38078595510133
CPU times: user 640 ms, sys: 206 ms, total: 845 ms
Wall time: 1min 4s
7. Full Code
The code of this tutorial can be found in my Github under this link.

